Section 1.3: Evaluating Limits Analytically
Formal Definition
Def: Let $f$ be a function defined on an open interval containing $c$ (except possibly at $c$), and let $L$ be a real number. Then $\displaystyle{\lim_{x \to c}}f(x) = L$ if for each $\varepsilon > 0$ there exists a $\delta > 0$ such that if $0 < \lvert x - c\rvert < \delta$ then $\lvert f(x)-L\rvert < \varepsilon$.
Theorem 1.1: Let $b$ and $c$ be real numbers and 𝑛 be a positive integer. Then
$\displaystyle{\lim_{x \to c}}b=b$ and $\displaystyle{\lim_{x \to c}}x=c$
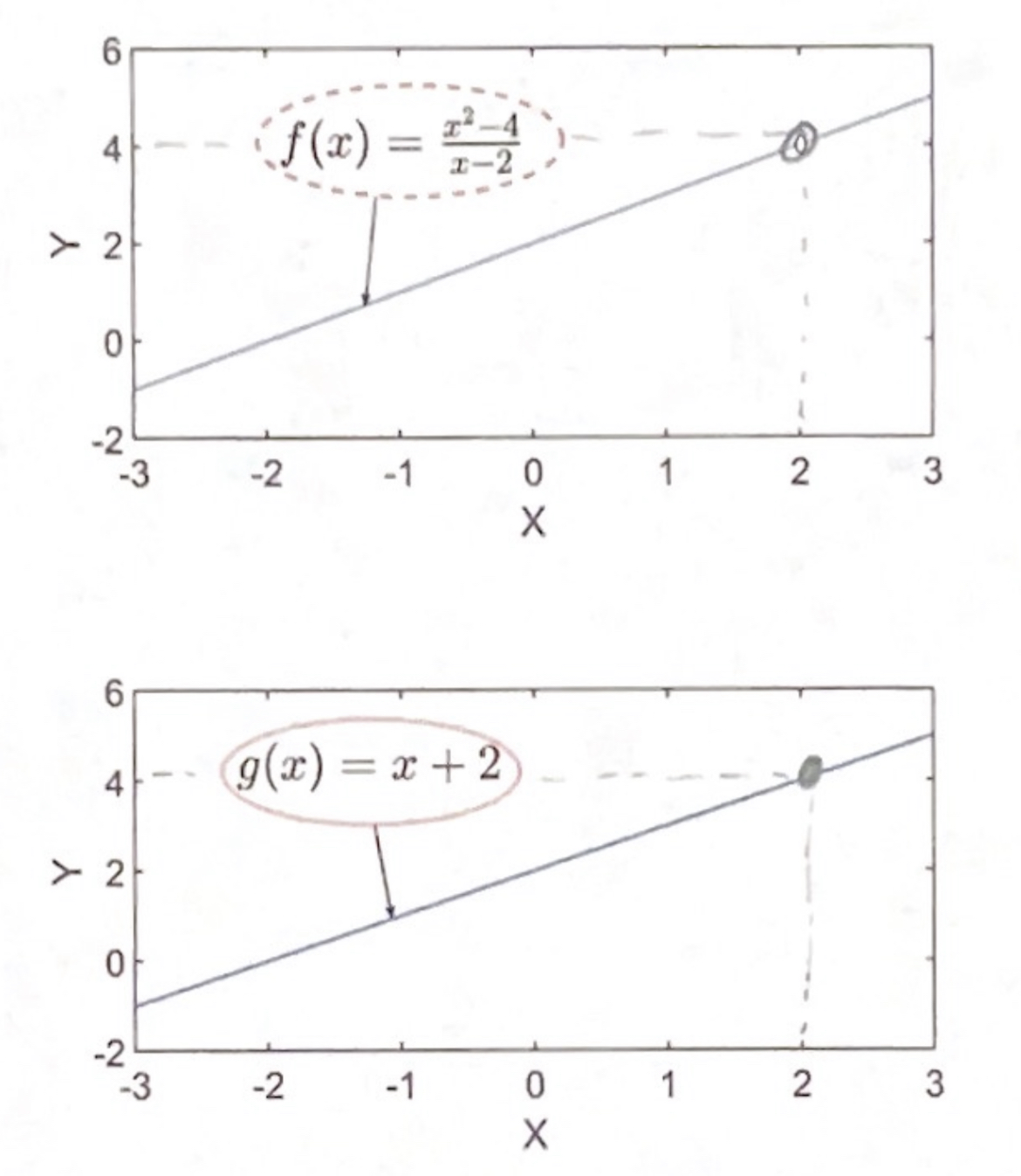
Functions like those in Theorem 1.1 in which $\displaystyle{\lim_{x \to c}}f(x)=f(c)$ can be evaluated using direct substitution.
Limit Laws
Theorem 1.2 The Limit Laws: Let $b$ and $c$ be real numbers, $n$ a positive integer, and $\displaystyle{\lim_{x \to c}}f(x)=L$ and $\displaystyle{\lim_{x \to c}}g(x)=K$
- Constant Multiple Law: $\displaystyle{\lim_{x \to c}}b * f(x)=b * L$
- Sum Law: $\displaystyle{\lim_{x \to c}}f(x)+g(x)=L+K$
- Product Law: $\displaystyle{\lim_{x \to c}} f(x) * g(x) = L * K$
- Quotient Law: $\displaystyle{\lim_{x \to c}}\frac{f(x)}{g(x)}=\frac{L}{K}$ if $K\neq0$
- Power Law: $\displaystyle{\lim_{x \to c}}f(x)^n=L^n$
- Root Law: If $n$ is odd or $n$ is even with $L>0$, $\displaystyle{\lim_{x \to c}}\sqrt[n]{f(x)}=\sqrt[n]{L}$
Ex 1: Find the limit $\displaystyle{\lim_{x \to 2}}3x^2-4x+5$
$\displaystyle{\lim_{x \to 2}}3x^2-4x+5=\displaystyle{\lim_{x \to 2}}3x^2-\displaystyle{\lim_{x \to 2}}4x+\displaystyle{\lim_{x \to 2}}5$
Constant Multiple Law:
$=3(\displaystyle{\lim_{x \to 2}}x)^2-4(\displaystyle{\lim_{x \to 2}})x+\displaystyle{\lim_{x \to 2}}5$
Theorem 1.1:
$=3(2)^2-4(2)+5$
$=12-8+5$
$= 9$
When to use Direct Substitution
Thm 1.3 Limits of Polynomials, Rational Functions, and Trigonometric Functions:
- If $p(x)$ is a polynomial, $\displaystyle{\lim_{x \to c}}p(x)=p(c)$.
- If $r(x)$ is a rational function given by $r(x)=\frac{p(x)}{q(x)}$ with $q(c)\neq0$, $\displaystyle{\lim_{x \to c}}r(x)=r(c)=\frac{p(c)}{q(c)}$.
- If $f(x)=sin(x)$,$cos(x)$,$tan(x)$, $cot(x)$, $sec(x)$, or $csc(x)$, $\displaystyle{\lim_{x \to c}}f(x)=f(c)$ for all $c$ in their domains.
Ex 2: Evaluate $\displaystyle{\lim_{x \to 5}}\frac{x^3-2x+3}{x-4}$
$\displaystyle{\lim_{x \to 5}}\frac{x^3-2x+3}{x-4}=\frac{5^3-2(5)+3}{5-4}=\frac{118}{1}$
Evaluating Limits Example
Ex 3: Evaluate $\displaystyle{\lim_{x \to 2}}\frac{x^3+6x^2+8x}{x+2}$
$\displaystyle{\lim_{x \to -2}}\frac{x^3+6x^2+8x}{x+2}=\frac{(-2)^3+6(-2)^2+8(-2)}{-2+2}=\frac{0}{0}$
$\displaystyle{\lim_{x \to -2}}\frac{x^3+6x^2+8x}{x+2}=\displaystyle{\lim_{x \to -2}}\frac{x(x^2+6x+8)}{x+2}=\displaystyle{\lim_{x \to -2}}\frac{x(x+2)(x+4)}{x+2}=\displaystyle{\lim_{x \to -2}}x(x+4)$
$\displaystyle{\lim_{x \to -2}}x(x+4)=-2(-2+4)=-4$
Thm 1.7 Simplifying Limits: Let $f(x)=g(x)$ for all $x\neq c$. If $\displaystyle{\lim_{x \to c}}g(x)$ exists, then $\displaystyle{\lim_{x \to c}}f(x)=\displaystyle{\lim_{x \to c}}g(x)$.
Warm Up Problem
Determine if the following equalities are true or false:
- (a) $\frac{(𝑥+2)^2}{(𝑥^3+4𝑥)}=\frac{(𝑥^2+4)}{(𝑥(𝑥^2+4))}=\frac{1}{𝑥}$ - False
- (b) $\frac{𝑥}{(\frac{𝑥}{3𝑥−2})}=\frac{x(3x-2)}{x}=3𝑥−2$ - True
- (c) $\frac{(\sqrt{x}+\sqrt{5}}{x+5}=\frac{\sqrt{x+5}}{x+5}=\frac{1}{\sqrt{x+5}}$ - False
More Examples
Ex 4: Find $\displaystyle{\lim_{x \to 3}}\frac{x^2-9}{x^2-7x+12}$
Ex 5: Evaluate $\displaystyle{\lim_{t \to 2}}\frac{\sqrt{t}-\sqrt{2}}{t-2}$
Ex 6: Evaluate $\displaystyle{\lim_{x \to 4}}\frac{\frac{1}{x}-\frac{1}{4}}{x-4}$
$\displaystyle{\lim_{x \to 4}}\frac{\frac{1}{x}-\frac{1}{4}}{x-4}=\displaystyle{\lim_{x \to 4}}\frac{\frac{4}{4x}-\frac{x}{4x}}{x-4}=\displaystyle{\lim_{x \to 4}}\frac{\frac{4-x}{4x}}{x-4}=\displaystyle{\lim_{x \to 4}}\frac{4-x}{4x}*\frac{1}{x-4}$
$=\displaystyle{\lim_{x \to 4}}\frac{4-x}{4x(x-4)}=\displaystyle{\lim_{x \to 4}}\frac{-(-4+x)}{4x(x-4)}=\displaystyle{\lim_{x \to 4}}\frac{-1}{4x}=\frac{-1}{16}$
Warm Up Problem
Draw a graph of a function $f(x)$ that is defined for all $x$ that satisfies the following:
$f(1)=5$, $\displaystyle{\lim_{x \to 1}}f(x)=2$, $f(4)=-3$, $\displaystyle{\lim_{x \to 4}}f(x)=f(x)$ does not exist
Trigonometric Limits
Thm 1.9 Special Trig Limits:
- (a) $\displaystyle{\lim_{\theta \to 0}}\frac{sin\theta}{\theta}=1$
- (b) $\displaystyle{\lim_{\theta \to 0}}\frac{1-cos\theta}{\theta}=0$
Thm 1.8 The Squeeze Theorem: If $h(x)\le f(x) \le g(x)$ for all $x$ in an open interval containing $c$, and if $\displaystyle{\lim_{x \to c}}h(x)=\displaystyle{\lim_{x \to c}}g(x)=L$, then $\displaystyle{\lim_{x \to c}}f(x)=L$.
Ex 7: Evaluate $\displaystyle{\lim_{x \to 0}}\frac{sin3}{2x}$
$\displaystyle{\lim_{x \to 0}}\frac{sin3}{2x}=\displaystyle{\lim_{x \to 0}}\frac{sin3 * \frac{3}{2}}{2x * \frac{3}{2}}=\frac{3}{2}\displaystyle{\lim_{x \to 0}}\frac{sin3}{3x}=\frac{3}{2}(1)=\frac{3}{2}$
$sin(ax) \neq sin(x)$
Warm Up Problem
Determine whether the following are True or False
- (1) If $\displaystyle{\lim_{x \to c}}g(x)$ exists, then $\displaystyle{\lim_{x \to c}}g(x)=g(c)$.
- (2) If $\displaystyle{\lim_{x \to c}}h(x)$ does not exist, then $h(c)$ is undefined.
- (3) If $f(c)=0$ and $g(c)=0$, then $\displaystyle{\lim_{x \to c}}\frac{f(x)}{g(x)}$ does not exist.
Guest Notes
Theorem 1.7: Let $c$ be a real number and let $f(x)=g(x)$ for all $x \neq c$ in a open interval containing $c$. If the limit $g(x)$ as $x$ approaches $c$ exists, then the limit of $f(x)$ also exists and
\[\displaystyle{\lim_{x \to c}} f(x) =\displaystyle{\lim_{x \to c}} g(x)\]Example: Evaluate
\[\displaystyle{\lim_{x \to c}}\frac{x^2-4}{x-2}\]Dividing Out Technique:
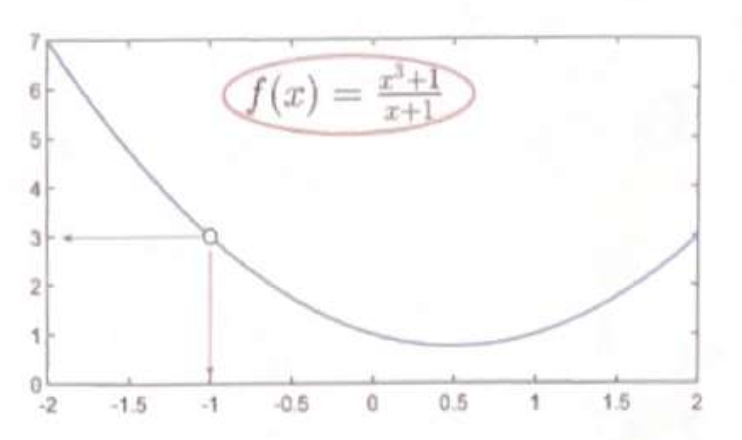
Consider the following limit
\[\displaystyle{\lim_{x \to -1}}\frac{x^3+1}{x+1}\] \[\displaystyle{\lim_{x \to -1}}\frac{x^3+1}{x+1}=\frac{-1+1}{-1+1}=\frac{0}{0}\] \[\displaystyle{\lim_{x \to -1}}\frac{x^3+1}{x+1}=\displaystyle{\lim_{x \to -1}}\frac{(x+1)(x^2-x+1)}{x+1}=\displaystyle{\lim_{x \to -1}}x^2-x+1\] \[(-1)+(+1)+1=3\] \[a^3+b^3=(a+b)(a^2-ab+b^2)\]Use graphically utility to check answer:
More example:
\[\displaystyle{\lim_{x \to 0}}\frac{x^3+3x}{x}=\displaystyle{\lim_{x \to 0}}\frac{x(x^2+3)}{x}=\displaystyle{\lim_{x \to 0}}x^2+3=3\]Rationalizing Technique: If the rational function involves radical expression and it is in indeterminate form, we have to rationalize either numerator or denumerator by multiplying and dividing by its conjugate.
Conjugate
\[\sqrt{x}+\sqrt{a}, \sqrt{x}-\sqrt{a}\] \[\sqrt{b}-\sqrt{c}, \sqrt{b}+\sqrt{c}\]Rationalize Numerator:
\[\displaystyle{\lim_{x \to 4}}\frac{\sqrt{x+5}-3}{x-4}\] \[\displaystyle{\lim_{x \to 4}}\frac{\sqrt{x+5}-3}{x-4}*\frac{\sqrt{x+5}+3}{\sqrt{x+5}+3}\] \[\displaystyle{\lim_{x \to 4}}\frac{(x+5)-9}{(x-4)(\sqrt{x+5}+3)}\] \[\displaystyle{\lim_{x \to 4}}\frac{x-4}{(x-4)(\sqrt{x+5}+3)}\] \[\displaystyle{\lim_{x \to 4}}\frac{1}{\sqrt{x+5}+3}\] \[=\frac{1}{6}\]Theorem 1.8: The Squeeze Theorem
If $h(x)\le f(x)\le g(x)$ for all $x$ in an open interval containing $c$, except possibly at $c$ itself.
\[\displaystyle{\lim_{x \to c}}h(x)=L=\displaystyle{\lim_{x \to c}}g(x)\]Then exist and is equal to $L$
\[\displaystyle{\lim_{x \to c}}f(x)\]Theorem 1.9: Two Special Trigonometric Limits
\[\displaystyle{\lim_{x \to 0}}\frac{sin(x)}{x}=1\] \[\displaystyle{\lim_{x \to 0}}\frac{1-cos(x)}{x}=0\]Look at the book at page 69
Evaluate the following limits
\[\displaystyle{\lim_{x \to 0}}\frac{tanx}{x}\] \[\displaystyle{\lim_{x \to 0}}\frac{sinx}{cosx*x}=\displaystyle{\lim_{x \to 0}}\frac{sinx}{x}*\displaystyle{\lim_{x \to 0}}\frac{1}{cosx}\] \[1 * 1 = 1\] \[\displaystyle{\lim_{x \to 0}}\frac{sin(4x)}{x}\] \[4\displaystyle{\lim_{x \to 0}}\frac{sin4x}{4x}\] \[1 * 4 = 4\]