Section 1.2: Finding Limits Graphically and Numerically
Informal Definition of a Limit and First Examples
Limit: $\displaystyle{\lim_{x \to c}}$ $f(x) = L$
$c = x$ value and $L = y$ value
A limit is arbitaritly number close to $L$ by testing numbers around $c$ on it’s left and right sides.
- Def: If a function $f(x)$ becomes arbitrarily close to a number $L$ as $x$ approaches $c$ from the right and from the left, then the limit of $f(x)$ as $x$ approaches $c$ is $L$, written as $\displaystyle{\lim_{x \to c}}$ $f(x) = L$.
-
Ex 1: Evaluate the function $f(x)=\frac{(x^2-4)}{(x-2)}$ at values near $x=2$ to estimate $\displaystyle{\lim_{x \to 2}}$ $f(x)$.
$\displaystyle{\lim_{x \to 2}} f(x)={\frac{(x^2-4)}{(x-2)}} = \frac{(2)^2-4}{2-2} = \frac{0}{0}$
$x$ $f(x)$ 1.9 3.9 1.99 3.99 1.999 3.999 2.001 4.001 2.01 4.01 2.1 4.1 So the limit of $x$ approaching 2 is about 4.
Find the limit as $x$ approachs to 3:
$\displaystyle{\lim_{x \to 3}} f(x)={\frac{(x^2-4)}{(x-2)}} = \frac{(3)^2-4}{3-2} = \frac{9-4}{3-2} = 5$
-
Ex 2: Estimate the limit $\displaystyle{\lim_{x \to 0}}$ where
$f(x)=\begin{cases}\frac{\cos x -1}{x} & if x\neq0 \ 4 & if x = 0 \ \end{cases}$
$f(0) = 4$
It’s possible for the limit not to match the actual point of the function:
$\displaystyle{\lim_{x \to c}} f(x)\neq f(c)$
$x$ $f(x)$ -0.5 0.2448 -0.1 0.04996 -0.01 0.0049 0.01 -0.0049 0.1 -0.04996 0.5 -0.2488 So the limit of $x$ approaching 0 is about 0.
$\displaystyle{\lim_{x \to 0}} f(x) = 0 $
Warm Up Problem
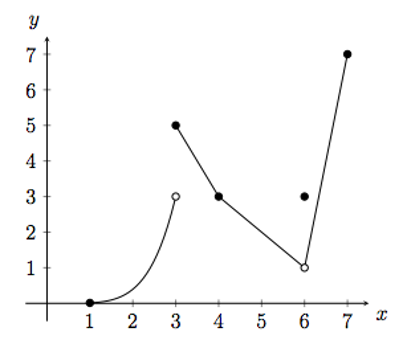
- Determine the value of the following limits of $f(x)$, if they exist:
- $\displaystyle{\lim_{x \to 3}}$ $f(x) = DNE$
- $\displaystyle{\lim_{x \to 4}}$ $f(x) = 3$
- $\displaystyle{\lim_{x \to 6}}$ $f(x) = 1$
- Remember that limits is the number that approaching and maybe not the number that is defined.
More Examples of Limits
-
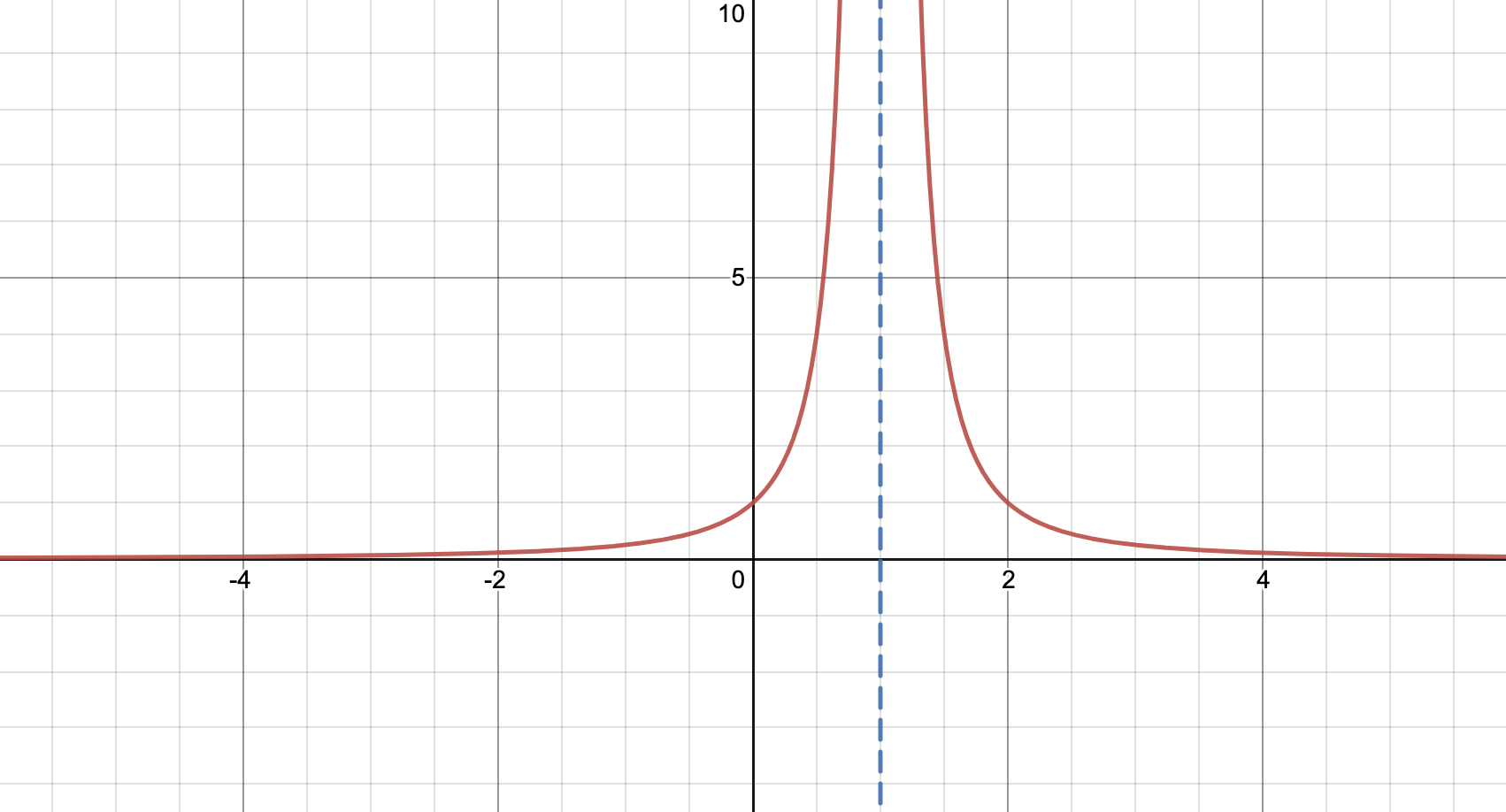
Ex 3: Estimate $\displaystyle{\lim_{x \to 1}}$ $f(x)$ $\frac{1}{x^2-2x+1}$
$x$ $f(x)$ 0.9 100 0.99 10000 0.999 1000000 1.001 1000000 1.01 10000 1.1 100 So the limit of $x$ approaching 1 does not exist. You can see this graphically:
-
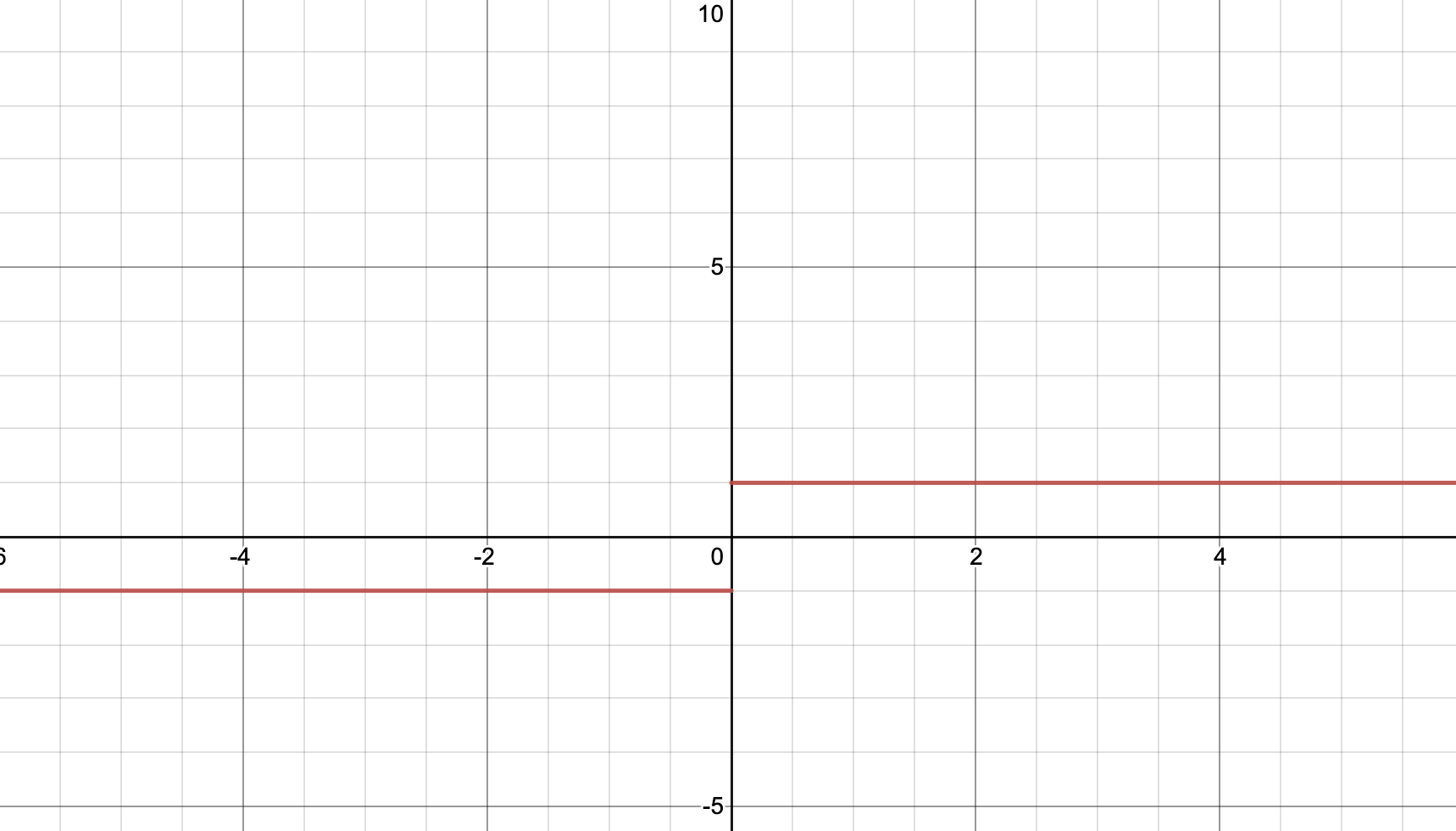
Ex 4: Find $\displaystyle{\lim_{x \to 0}}$ $\frac{\lvert x\rvert}{x}$ using its graph then by simplifying the equation.
This limit does not exist since the left and the right have different values.
-
Ex 5: Fill in the tables of values to estimate the limit: $\displaystyle{\lim_{x \to 0}}$ $\sin \frac{1}{x}$
$x$ $\sin \frac{1}{x}$ $x$ $\sin \frac{1}{x}$ $x$ $\sin \frac{1}{x}$ 2/$\pi$ 1 2/3$\pi$ -1 1/$\pi$ 0 2/5$\pi$ 1 2/7$\pi$ -1 1/5$\pi$ 0 2/13$\pi$ 1 2/31$\pi$ -1 1/10$\pi$ 0 2/101$\pi$ 1 2/99$\pi$ -1 1/100$\pi$ 0 The limit does not exist because the function continually oscillates between -1 and 1 as $x\ge0$.
Why a limit may not exist or be infinite?
- $f(x)$ increases or decreases (not both) without bound as ${x \to c}$.
- $f(x)$ approaches two different numbers from the right and left sides of $c$.
- $f(x)$ oscillates between two fixed values as ${x \to c}$.