Section 1.1 - Preview of Calculus
Warm Up Problem
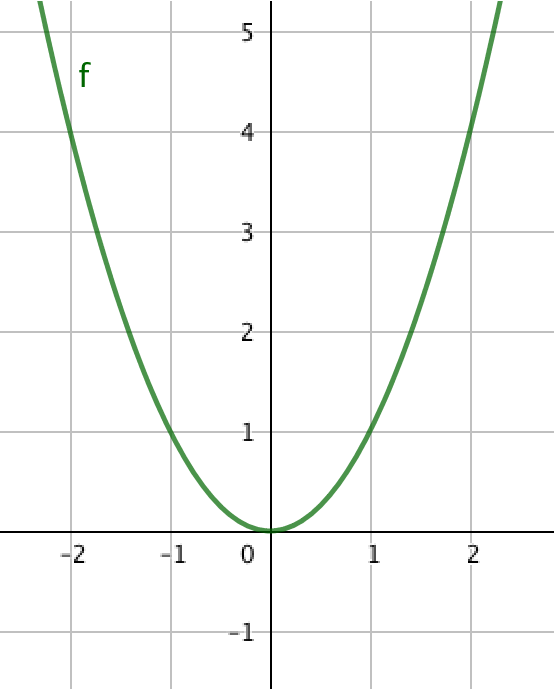
Calculate the slope of the secant line of $f(x)=x^2$ from the point (1,1) to the point (2,4).
$\frac{4-1}{2-1}=\frac{3}{1}=3=slope$
$\frac{f(x_2)-f(x_1)}{x_2-x_1}$
- Secant Line - A Line with 2 points on the curve.
- Tangent Line - A line that intersects $f(x)$ af $f$ and nowhere else hear $P$.
Motivating Example
Can we determine the slope of the graph $f(x)=x^2$ at the point (1,1)?
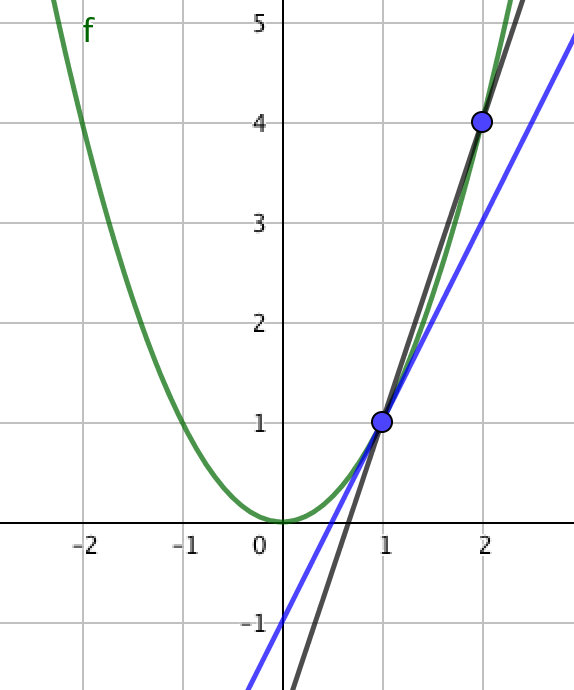
$(1, 1)$ to $(1.5, 2.25)$
$\frac{2.25-1}{1.1-1}=\frac{.21}{.1}=2.1 slope$
The Slope of the Tangent Line: $m=2$
$(1, 1)$ to $(x, f(x)):\frac{f(x)-1}{x-1}=\frac{x^2-1}{x-1}$
$\displaystyle{\lim_{x \to 1}}=\frac{x^2-1}{x-1}=2$
$\frac{x^2-1}{x-1}=\frac{(x+1)(x-1)}{x-1}=x+1$
Preview of Calculus
- One of our first goals: Finding the slope of a curve $y=f(x)$.
- Need to find a the slope of a tangent line at a point $P$: a line that intersects $f(x)$ at $P$ and nowhere else near $P$.
- We do this by approximating the tangent line with secant lines: lines between two points on the curve.
- Def: Calculus is the mathematical study of change.